新课程下的数学探索性问题类型综述
论文摘要:新课程下的探索性问题既能充分考查学生的基础知识的掌握熟练程度,又能较好地考查学生的观察、分析、比较、概括能力,发散思维能力,探索发现能力,独立创新能力和解决实际问题的能力等.条件探索型常用“执果索因”法,结论探索型常用“分类讨论”的思想方法,存在性探索型常用“假设存在”方法,规律探索型常用“类比、迁移”方法来解决.
论文关键词:新课程,探索性问题,解题思路
我们国家《新课程标准》明确指出,要在数学教学过程中充分体现出学生“经历观察、操作、试验、调查、推理等数学过程,发展合情推理能力,初步的演绎推理能力,能有条理地、清晰地阐述自己的观点;通过观察、操作、归纳、类比、推断等数学活动,体验数学问题的探索性和挑战性,感受数学思考过程的条理和数学结论的确定性”.可以看出新课程对培养学生的探索性能力的要求.新课程下的探索性问题既能充分考查学生的基础知识的掌握熟练程度,又能较好地考查学生的观察、分析、比较、概括能力,发散思维能力,探索发现能力,独立创新能力和解决实际问题的能力等.我认为凡是具有以下特征之一的都是数学探索性问题:
一结论探索
给出题设条件,但题目结论未指明,或者只给出结论范围,要解题者自己进行判断和选择.它的解题思路是执因索果、分类讨论,从所给条件出发,通过观察、试验、分析、归纳,猜想等诸多手段,由浅人深,逐步探求出相关的结论.
例如在我国江汉平原上有四个村庄恰好落在边长为2km的正方形顶点上,现需要建立一个使得任何两个村庄都可有通道的道路网.请合理设计一个道路网,使它的总长度不超过5km(取 =1.14142,
=1.14142, =1.17321)
=1.17321)
分析:这是一实际问题的“结论探索题”,首先应发挥你的想象力,列举一些常规方案,然后在观察与试验中逐步逼近题目的有关要求,在逐渐深人的过程中得出结论.对于如图(a)所示的四个村庄,我们最容易想到的方案为:
(l)若沿正方形四边修建,总长度为8km,不符合要求.
(2)若沿两对角线修建,总长度为4 >5(km),也不合要求.
>5(km),也不合要求.

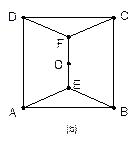
(3)由平面几何知识可知,正方形内任一点P到四顶点距离之和,以选取对角线的交点o为最短,但由于情形(2)已被否定,故应考虑增加公共道路,又因为正方形既是轴对称图形,又是中心对称图形,所以考虑道路EF的选择,如图(b)所示,设OE=OF=x,其中0≤x≤1,则道路总长度y=2x+4 ,由题目要求,y≤5,得48x-40x+7≤0,解得
,由题目要求,y≤5,得48x-40x+7≤0,解得 ,此范围内x均符合要求.
,此范围内x均符合要求.
二条件追溯
条件探索题的结论明确而条件不完备,需要依据题意找出结论成立所具备的条件.它的解题思路是执果索因,从结论出发,可将结果看成条件,通过观察、试验、分析、归纳,猜想等诸多手段,由浅人深,逐步探求结论所需要的条件.
例如设x、y、z是倒数和为1的三个实数,试问这三数之间存在什么关系,方能保证x、y、z中至少一个为1.
分析一:由于题设条件不充分,需进一步完备之,为此,可将结论视为条件,执果寻因,探寻所需的条件.要使x、y、z中至少有一个为1,即(1-x)(1-y)(1-z)=0也就是1-x-y-z+xy+yz+zx-xyz=0
又已知有:
即xy+yz+zx-xyz=0
从而只要有1-x―y―z=0,即x+y+z=1.这就是所求的x、y、z间的关系.
三规律探索
规律探索型问题是指由给出的几个具体的结论来探求与它相关的一般性的结论的问题.它的解题思路类比、迁移,从题设条件得出,通过观察,实验分析,比较,归纳,猜想,探索出一般性的规律,然后对所归纳,猜想的结论进行证明,对于一些较为复杂的问题,可将问题分类进行讨论,然后进行分析归纳出一般性的规律,解这类题的关键是正确的归纳和猜想,证明猜想的方法是数学归纳法和演绎推理.
例如阅读下列材料:
关于x方程:
 +
+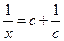 ,解是x=c,x=
,解是x=c,x= ,
,
 解是x=c,x=
解是x=c,x= ,
,
 +
+ ,解是x=c,x=
,解是x=c,x= ,
,
 +
+ ,解是x=c,x=
,解是x=c,x= .
.
(1)请观察上述方程与解的特征,比较关于x方程 +
+ (
( ≠0)与它们的关系,猜想它的解是什么,并利用“方程的解”的概念进行验证.
≠0)与它们的关系,猜想它的解是什么,并利用“方程的解”的概念进行验证.
(2)由上述的观察、比较、猜想、验证,可以得出什么结论,请用你得出的结论,解关于x方程x十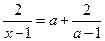 .
.
分析:先分析每个式子左右端的各数字间的变化规律及由各式得出的结果的变化规律,结合上下式,再分析各式数字间的变化规律,然后探求、发现变化规律,并且直接利用这个规律解题.
四条件结论变换
先给出一个封闭性的问题,然后改变题设条件探讨结论将会发生怎样的变化,或改变题目结论探讨基本条件要发生怎样的变化.本题的解题思路是,通过观察、类比、归纳、猜想.在变化中抓住不变,找出规律,从而一举击破.
例如如图1,已知⊙O和⊙O 都经过点A和点,直线PQ切⊙O
都经过点A和点,直线PQ切⊙O 点P,交⊙O
点P,交⊙O 于点Q、M,交AB的延长线于点N.
于点Q、M,交AB的延长线于点N.
(1)求证:PN=NM·NQ.
(2)若M是PQ的中点,设MQ=x,MN=y,求证:x=3y.
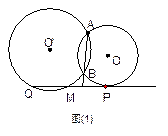



(3)若⊙O 不动,把⊙O向右向左平移,分别得到图2、图3、图4,请你判断(直接写出判断结论,不需证明):
不动,把⊙O向右向左平移,分别得到图2、图3、图4,请你判断(直接写出判断结论,不需证明):
①(1)题结论是否仍然成立?
②在图2中,(2)题结论是否仍然成立?
在图3、图4中,若将(2)题条件改为:M是PN的中点,设MQ=x,MN=y,则x=3y的结论是否仍然成立?
分析:本题要求学生根据图形的变化及变式、探求新条件下的新结论,使学生体会在某些几何图形中存在“形变质不变的规律”,从而锻炼考生思维的灵敏性和深刻性
五存在探索
这类问题最常见,1981年全国高考数学试题已出现.存在探索问题是指在给定条件下,判断某种数学现象是否存在或某个结论是否出现的问题.它的解题思路是假设存在,先假设所探求的对象存在或结论成立.以此假设为前提进行运算或逻辑推理,由此推出之后,若假定不成立,则得到“否定的”结论,即不存在,如果推理不出现矛盾,并求出了题设范围内的数值或图形,就得到肯定的结论,即得到存在的结果,这与反正法的思路极为相似.
例如已知抛物线y=x十(m一2)x十3(m十1).
(1)求证:不论m为何实数,此抛物线与x轴总有公共点;
(2)设抛物线与x轴交于A,B两点(点A在点B的左侧)与y轴交于点C,试问∠CAB与∠CBA这两个角中是否可能存在钝角?如果存在,试求m允许取值的范围;如果不存在,请说明理由.
分析:(1)欲探索∠CAB与∠CBA中是否可能存在钝角,也应根据数形结合思想,分两种情况,分别讨论A,B两点同在原点的左侧或同在原点的右侧,利用一元二次方程的根与系数的关系结合根的判别式,列出不等式组,即可求出m取值的范围.
(2)在∠CAB与 ∠CBA中可能存在一个钝角,设∠CAB与∠CBA有一个钝角,则点A,B必是在原点同侧.
∠CBA中可能存在一个钝角,设∠CAB与∠CBA有一个钝角,则点A,B必是在原点同侧.
以上几种常用的探索性问题的类型的解题思路明确了解.明确了条件探索型常用“执果索因”法,结论探索型常用“分类讨论”的思想方法,存在性探索型常用“假设存在”方法,规律探索型常用“类比、迁移”方法来解决,条件结论变换型抓住“形变质不变的规律”.但从解题来看,它不具有定向的解题思路,因此我们要有合情合理的分析,要把归纳与演绎协调配合起来,把直觉发现和逻辑推理相结合,注重数学思想方法的综合应用.通过探索性数学问题的解题活动,不仅促进数学知识和数学方法的巩固和掌握,更有利地培养了同学们的探究精神及创造才能.
参考文献
1 汤服成主编.中学数学解题思想方法[M].广西师范大学出版社. 2005.
2 卜以楼.数学探索题的归类评析[J].考试评析. 2002
3 陈铁军. 黄爱民2005年高考数学探究性命题的求解策略[J].高中数学教与学 2006.
4 王爱笑.初中数学探究性问题的分类及解题策略[J].中学教研. 2004.
5 陈中峰.初中数学探究性问题的解法[J].教学研究. 2006.
6 尹友军. 浅析高考数学中的数列综合问题[J]. 数学通讯. 2007,(07).
论文关键词:新课程,探索性问题,解题思路
我们国家《新课程标准》明确指出,要在数学教学过程中充分体现出学生“经历观察、操作、试验、调查、推理等数学过程,发展合情推理能力,初步的演绎推理能力,能有条理地、清晰地阐述自己的观点;通过观察、操作、归纳、类比、推断等数学活动,体验数学问题的探索性和挑战性,感受数学思考过程的条理和数学结论的确定性”.可以看出新课程对培养学生的探索性能力的要求.新课程下的探索性问题既能充分考查学生的基础知识的掌握熟练程度,又能较好地考查学生的观察、分析、比较、概括能力,发散思维能力,探索发现能力,独立创新能力和解决实际问题的能力等.我认为凡是具有以下特征之一的都是数学探索性问题:
一结论探索
给出题设条件,但题目结论未指明,或者只给出结论范围,要解题者自己进行判断和选择.它的解题思路是执因索果、分类讨论,从所给条件出发,通过观察、试验、分析、归纳,猜想等诸多手段,由浅人深,逐步探求出相关的结论.
例如在我国江汉平原上有四个村庄恰好落在边长为2km的正方形顶点上,现需要建立一个使得任何两个村庄都可有通道的道路网.请合理设计一个道路网,使它的总长度不超过5km(取
 =1.14142,
=1.14142, =1.17321)
=1.17321)分析:这是一实际问题的“结论探索题”,首先应发挥你的想象力,列举一些常规方案,然后在观察与试验中逐步逼近题目的有关要求,在逐渐深人的过程中得出结论.对于如图(a)所示的四个村庄,我们最容易想到的方案为:
(l)若沿正方形四边修建,总长度为8km,不符合要求.
(2)若沿两对角线修建,总长度为4
 >5(km),也不合要求.
>5(km),也不合要求.
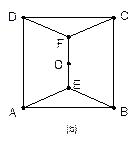
(3)由平面几何知识可知,正方形内任一点P到四顶点距离之和,以选取对角线的交点o为最短,但由于情形(2)已被否定,故应考虑增加公共道路,又因为正方形既是轴对称图形,又是中心对称图形,所以考虑道路EF的选择,如图(b)所示,设OE=OF=x,其中0≤x≤1,则道路总长度y=2x+4
 ,由题目要求,y≤5,得48x-40x+7≤0,解得
,由题目要求,y≤5,得48x-40x+7≤0,解得 ,此范围内x均符合要求.
,此范围内x均符合要求.二条件追溯
条件探索题的结论明确而条件不完备,需要依据题意找出结论成立所具备的条件.它的解题思路是执果索因,从结论出发,可将结果看成条件,通过观察、试验、分析、归纳,猜想等诸多手段,由浅人深,逐步探求结论所需要的条件.
例如设x、y、z是倒数和为1的三个实数,试问这三数之间存在什么关系,方能保证x、y、z中至少一个为1.
分析一:由于题设条件不充分,需进一步完备之,为此,可将结论视为条件,执果寻因,探寻所需的条件.要使x、y、z中至少有一个为1,即(1-x)(1-y)(1-z)=0也就是1-x-y-z+xy+yz+zx-xyz=0
又已知有:

即xy+yz+zx-xyz=0
从而只要有1-x―y―z=0,即x+y+z=1.这就是所求的x、y、z间的关系.
三规律探索
规律探索型问题是指由给出的几个具体的结论来探求与它相关的一般性的结论的问题.它的解题思路类比、迁移,从题设条件得出,通过观察,实验分析,比较,归纳,猜想,探索出一般性的规律,然后对所归纳,猜想的结论进行证明,对于一些较为复杂的问题,可将问题分类进行讨论,然后进行分析归纳出一般性的规律,解这类题的关键是正确的归纳和猜想,证明猜想的方法是数学归纳法和演绎推理.
例如阅读下列材料:
关于x方程:
 +
+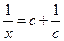 ,解是x=c,x=
,解是x=c,x= ,
, 解是x=c,x=
解是x=c,x= ,
, +
+ ,解是x=c,x=
,解是x=c,x= ,
, +
+ ,解是x=c,x=
,解是x=c,x= .
.(1)请观察上述方程与解的特征,比较关于x方程
 +
+ (
( ≠0)与它们的关系,猜想它的解是什么,并利用“方程的解”的概念进行验证.
≠0)与它们的关系,猜想它的解是什么,并利用“方程的解”的概念进行验证.(2)由上述的观察、比较、猜想、验证,可以得出什么结论,请用你得出的结论,解关于x方程x十
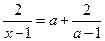 .
.分析:先分析每个式子左右端的各数字间的变化规律及由各式得出的结果的变化规律,结合上下式,再分析各式数字间的变化规律,然后探求、发现变化规律,并且直接利用这个规律解题.
四条件结论变换
先给出一个封闭性的问题,然后改变题设条件探讨结论将会发生怎样的变化,或改变题目结论探讨基本条件要发生怎样的变化.本题的解题思路是,通过观察、类比、归纳、猜想.在变化中抓住不变,找出规律,从而一举击破.
例如如图1,已知⊙O和⊙O
 都经过点A和点,直线PQ切⊙O
都经过点A和点,直线PQ切⊙O 点P,交⊙O
点P,交⊙O 于点Q、M,交AB的延长线于点N.
于点Q、M,交AB的延长线于点N.(1)求证:PN=NM·NQ.
(2)若M是PQ的中点,设MQ=x,MN=y,求证:x=3y.
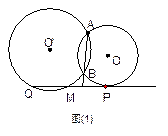



(3)若⊙O
 不动,把⊙O向右向左平移,分别得到图2、图3、图4,请你判断(直接写出判断结论,不需证明):
不动,把⊙O向右向左平移,分别得到图2、图3、图4,请你判断(直接写出判断结论,不需证明):①(1)题结论是否仍然成立?
②在图2中,(2)题结论是否仍然成立?
在图3、图4中,若将(2)题条件改为:M是PN的中点,设MQ=x,MN=y,则x=3y的结论是否仍然成立?
分析:本题要求学生根据图形的变化及变式、探求新条件下的新结论,使学生体会在某些几何图形中存在“形变质不变的规律”,从而锻炼考生思维的灵敏性和深刻性
五存在探索
这类问题最常见,1981年全国高考数学试题已出现.存在探索问题是指在给定条件下,判断某种数学现象是否存在或某个结论是否出现的问题.它的解题思路是假设存在,先假设所探求的对象存在或结论成立.以此假设为前提进行运算或逻辑推理,由此推出之后,若假定不成立,则得到“否定的”结论,即不存在,如果推理不出现矛盾,并求出了题设范围内的数值或图形,就得到肯定的结论,即得到存在的结果,这与反正法的思路极为相似.
例如已知抛物线y=x十(m一2)x十3(m十1).
(1)求证:不论m为何实数,此抛物线与x轴总有公共点;
(2)设抛物线与x轴交于A,B两点(点A在点B的左侧)与y轴交于点C,试问∠CAB与∠CBA这两个角中是否可能存在钝角?如果存在,试求m允许取值的范围;如果不存在,请说明理由.
分析:(1)欲探索∠CAB与∠CBA中是否可能存在钝角,也应根据数形结合思想,分两种情况,分别讨论A,B两点同在原点的左侧或同在原点的右侧,利用一元二次方程的根与系数的关系结合根的判别式,列出不等式组,即可求出m取值的范围.
(2)在∠CAB与
 ∠CBA中可能存在一个钝角,设∠CAB与∠CBA有一个钝角,则点A,B必是在原点同侧.
∠CBA中可能存在一个钝角,设∠CAB与∠CBA有一个钝角,则点A,B必是在原点同侧.以上几种常用的探索性问题的类型的解题思路明确了解.明确了条件探索型常用“执果索因”法,结论探索型常用“分类讨论”的思想方法,存在性探索型常用“假设存在”方法,规律探索型常用“类比、迁移”方法来解决,条件结论变换型抓住“形变质不变的规律”.但从解题来看,它不具有定向的解题思路,因此我们要有合情合理的分析,要把归纳与演绎协调配合起来,把直觉发现和逻辑推理相结合,注重数学思想方法的综合应用.通过探索性数学问题的解题活动,不仅促进数学知识和数学方法的巩固和掌握,更有利地培养了同学们的探究精神及创造才能.
参考文献
1 汤服成主编.中学数学解题思想方法[M].广西师范大学出版社. 2005.
2 卜以楼.数学探索题的归类评析[J].考试评析. 2002
3 陈铁军. 黄爱民2005年高考数学探究性命题的求解策略[J].高中数学教与学 2006.
4 王爱笑.初中数学探究性问题的分类及解题策略[J].中学教研. 2004.
5 陈中峰.初中数学探究性问题的解法[J].教学研究. 2006.
6 尹友军. 浅析高考数学中的数列综合问题[J]. 数学通讯. 2007,(07).
关键字:教育,广西
上一篇:简述对外汉语词汇教学的方法途径
下一篇:简析如何引导学生轻松写作

